7 The Rug Rat Race
7.1 Time Diaries
Figure 7.1 plots a somewhat puzzling finding from Ramey and Ramey (2010). The figure shows the amount of hours per week mothers spend on childcare over time. For both college-educated and less-than-college-educated mothers, time spent on childcare rose dramatically in the early 1990s?
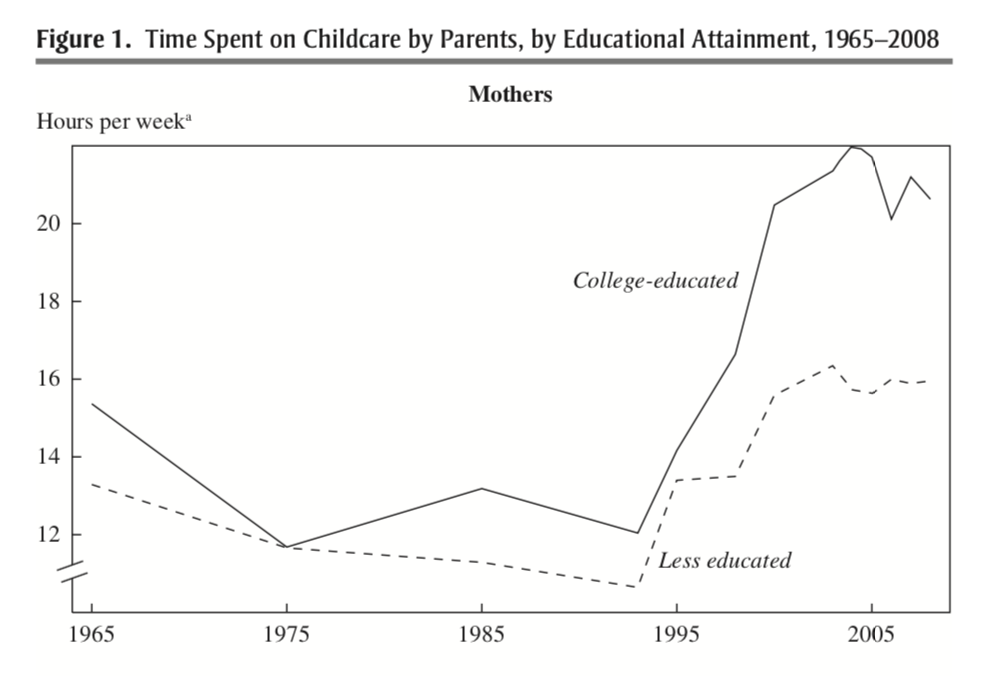
Figure 7.1: Time Spent on Childcare by Parents, by Educational Attainment, 1965-2008
This rise occurs for both college-educated and less-educated mothers, but the rise is especially dramatic for college-educated mothers. Why is this puzzling? Well, this is a time period in which the returns to education were increasing a lot. In other words, these college-educated mothers had a lot to gain from working in the labor market, but in the data, we find they are spending more time on childcare. In this section of the course, we will explore why.
In order to explore this question we will use data from the American Time Use Survey (ATUS). This is a survey administered by the Bureau of Labor Statistics, and agency that collects many important statistics concerning the U.S. economy.
The data is based on "time diaries" which are detailed descriptions of the activities in a given day. For example, if the interview was held on a Tuesday, the individual would report everything they did on Monday (from 4 AM Monday to 4 AM Tuesday). This is a useful survey technique to get an accurate representation of how much time people spend on various activities.
Before digging into the data, however, we are going to learn a bit more about the R programming language. In particular, in this chapter we will cover some important functions for data wrangling.
7.2 Conditional Statements
The basic idea behind conditional statements is that sometimes in R we want to execute some code, but only if a certain condition is true. Conditional statements are incredibly important in all programming languages. For example, when you type something on a computer and get and error statement, that is a conditional statement at work. A certain condition was met (some error in this case), so the computer output an error message.
The way we will implement this idea in R is to use if statements. The general syntax for if statements is:
It might be a bit easier to understand this syntax with a simple example. To begin, we are going to create an object in R called door which is equal to locked.
door <- "locked"Now, we are going to write some code to return a message if the object door is indeed locked.
if (door=="locked") {
print("sorry, you need a key to enter")
}
[1] "sorry, you need a key to enter"What is R doing here? Well, because we have assigned the value locked to the object door, the logical statement in parentheses door=="locked" is TRUE. Therefore, if we run this section of code, the code inside the curly brackets {} will be executed. In this case, the code just prints a message.
What happens if we change the value of door to unlocked. Well, in that case door=="locked" is no longer TRUE. Therefore, the code inside the brackets will not be executed.
door <- "unlocked"
if (door=="locked") {
print("sorry, you need a key to enter")
}Let's try another example. Say we take a random draw from three numbers: -1, 0, and 1. We can take a random draw from this list of numbers by using the sample function:
The part of the code -1:1 controls what numbers will be drawn. If you type -1:1 in R, you will see it prints out the numbers -1,0, and 1. The second part of the code ,1 tells R how many random samples to take. In this case, just 1. So overall, this code is simply setting x equal to either -1, 0, or 1 and doing so randomly.
So now let's write a conditional statement that depends on the outcome of x. Let's write some code that returns the absolute value of x, but only if x is less than zero.
if (x<0){
abs(x)
}Next, let's discuss else statements. Sometimes, we want to execute certain code if the statement is TRUE, but some other code if it is FALSE. For example, in our first example, imagine if the door object is not equal to locked then we want R to print out the message Please Come in!. The way we can do this in R is with an else statement:
door <- "locked"
if (door=="locked"){
print("Sorry, you need a key to enter")
} else {
print("Please Come in!")
}
[1] "Sorry, you need a key to enter"Since we set door<-"locked", the first statement door=="locked" is TRUE. Therefore, the code inside the first curly brackets was executed. Now, let's change door to unlocked and see how this changes the output.
door <- "unlocked"
if (door=="locked"){
print("Sorry, you need a key to enter")
} else {
print("Please Come in!")
}
[1] "Please Come in!"So now the first statement door=="locked" is FALSE. Therefore, R executes the code after the else {}.
There are a few important notes about conditional statements before we move on. First, the else must appear on the same line as the end curly bracket }. If it doesn't, then R doesn't know what logical statement to connect the else to. Second, R will execute the code after the else brackets if door=="locked" is FALSE for any reason.
For example, imagine I set door <- "Locked". While it might look like the first logical statement door=="locked" is true, R is case sensitive. Therefore, in this case, the statement door=="locked" is FALSE. This implies that R will print out the words Please Come in!.
7.3 For Loops
In data analysis, we often find ourselves performing the same operation many times. We might be performing the same analysis for different variables or performing the same calculation for many different numbers.
One way to perform this analysis is through writing scripts with many, many lines of code. Much of the code might be exactly the same, but simply changes a single number or variable. An alternative way to perform this computation is through loops. Although we are learning how to implement loops in R, loops are a concept that you should be aware of in any programming language.
The general form for a loop in R is given below:
The for tells R this will be a for loop. Some set of things will depend on exactly what you are trying to do. Often, it will be a list of numbers. The next part of the code { tells R that everything that follows is part of the loop. The end curly bracket } tells R that the loop is over.
To understand these concepts more concretely. We are going to go through a simple example. Let's imagine that someone has demanded you use R to print out 2*i for i equal to 1, 2, 3, 4, and 5. In simpler language, multiply each number between 1 and 5 by 2 and then print out the result. We are going to perform this in what we will call the brute force method.
First, let's print out 2*1
So why did we code this in such a roundabout way? Why not directly type 2*1. Well, once we go through the loop it will become clear why we are coding this in a somewhat roundabout way. What you need to understand now is exactly what the code is doing. First, it is creating an object named i that is equal to 1. Then, it is multiplying that object by 2 and printing out the result. Now, we have to do this for the number 2.
Note that the second part of the code print(2*i) is exactly the same as before. That will be key when we are writing our loop. We can continue to do this for the rest of the numbers
In each block of code, the only thing changing is what i is equal to. Well, this is exactly what a loop does.
When we type for (i in 1:5) we are telling R to execute print(2*i) 5 times. The first time, i==1. This is referred to as the first iteration of the loop. Once it has executed the code for i==1, it should move on to i==2. This is the second iteration of the loop.
The great thing about this is that it can greatly increase the efficiency of our coding. For example, imagine we wanted to print out 2*i for i=1:100. If we go the brute force way, that would be 200 lines of code (first setting i equal to the given number and then executing the code). But with the loop, only one thing changes: in the first line we simply type for (i in 1:100).
In this example we are iterating over a list of numbers from 1 to 5. You can also iterate over other objects in R. For example, instead of iterating over a sequence of numbers, you can iterate over a vector.
In this loop, in the first iteration, i is equal to 3. In the second iteration i is equal to 10. In the third i is equal to 99.
Next, we are going to go through an example that loops over words instead of numbers. In this example, we are going to print out a to do list. Let's say we need to do three sets of homework assignments: math, reading, and writing. To start this example, let's create a vector of the assignments we need to do:
homework <- c("math", "reading", "writing")We can loop over the contents of this vector in order to print out a to-do list.
We introduced a few new things here, so let's go through the code slowly. First, instead of looping over numbers here, we are looping over words. In the first iteration i is equal to the first entry of the vector homework. Therefore, i is equal to math in the first iteration.
Next, we have used a knew function cat(). This function concatenates and prints. Therefore, if we type cat("Do",i) what you should interpret (in the first) iteration is that we are forming the sentence Do Math. The last part ,"\n" is telling R to display the next text a line down.. When you want to skip a line in a word document, you just press Enter. In R, you can type "\n". If you are still unsure what "\n" is doing, you should try to take it out of the code and see how the result looks.
In this example, we are looping over the words in homework. An alternative way to write this loop out will take advantage of indexing. The following code performs the exact same process as above, it is just coded in a slightly different way.
In this loop, we are again looping over numbers. length(homework) is equal to 3. So we are looping over the numbers 1 to 3. In the first iteration, we are concatenating the words "Do" and homework[1]. Since homework[1] is equal to Math, we are retrieving the exact same output as before.
So why would we want to code this loop in this way? Well, in this setting, it doesn't really matter how you write the code. However, that won't always be the case. Using the loop index (i) in order to subset vectors or data frames is a very common practice, so it is important to be exposed to this aspect of loops as well.
7.4 For Loops (Data)
Next, we are going to use for loops to make calculations in our data. To remind you, our empirical application is going to study how time spent on childcare, particularly for mothers, has changed over time. To begin, we are going to load in data from the American Time Use Survey.
As you can see, this is a pretty large dataset. There are 106,020 observations and 54 variables. Because this data is so large, we are first going to explain a subset of variables that we will be focusing on. Our goal is to compute time spent on childcare over time for mothers. The variable mother2 is an indicator variable that is equal to one if the individual is a mother with a child currently living in the household. age is holds the age of the individual. childtot is the total hours spent on childcare in a week. dataset actually holds the year the data was collected. Different years come from datasets. This will be important to keep in mind going forward with the analysis.
Our goal is to follow the Ramey and Ramey (2010) analysis as closely as possible. In order to do this, we are going to make a number of restrictions in our data so that we have the same sample of individuals studied by Ramey and Ramey (2010). This will involve restricting to mothers between ages 25 and 34 with a child in the household. In terms of the variables in the data frame, these are individuals such that age>=25 & age<=34 & mother2==1. This is a logical statement composed of three statements, strung together by & operators. Therefore, in order to be TRUE, every individual statement must be TRUE. You should be able to convince yourself that this statement is only TRUE for mothers between the ages of 25-34.
The way we can subset to these individuals is through the subset command.
mothers2534 <- subset(rr, mother2==1 & age>=25 & age<=34)Now we have a data frame restricted to the sample we are analyzing. Our goal is to compute the average amount of childtot over years (in our case, over different values of the variable dataset). Therefore, what we need next is a list of the years in the data frame.
Luckily, there is a function unique() that will come in handy here. unique() retrieves list of the unique values of a variable. In other words, if we type unique(rr$dataset) we will get a list of all the years in the data frame.
years <- unique(mothers2534$dataset)
years
[1] 1965 1975 1985 1993 1998 2003 2004 2005 2006 2007 2008So we are going to write a loop and iterate over the years. Before writing the full loop, let's make sure we understand how to code this for the first iteration. First, let's set i equal to one.
i <- 1 Next, let's subset the data so that we create a dataframe that only contains observations such that dataset==years[i]. Since i is currently equal to 1, this will subset the data to observations from 1965.
sub <- subset(mothers2534, dataset==years[i])Since the data frame sub only contains observations from 1965, we can simply take the average of childtot within this data frame to retrieve the average amount of hours spent on childcare per week in 1965.
When we actually go to iterating over a loop, we will want to keep track of what each number printed out corresponds to. Therefore, let's use the cat() function to clarify exactly what is being printed out. We are actually going to print out two things. First, we are going to print out the year we are studying. Then, we are going to print out the average childcare in that year.
# prints out year
cat("Year", years[i],"\n")
Year 1965
# prints out average childcare for this group
cat("Average childcare per week:", mean(sub$childtot),"\n")
Average childcare per week: 13.82249 Now that we have written all the code for i<-1, we just need to put this code inside a loop that loops over from 1 to the total number of years. The total number of years is given by length(years):
for (i in 1:length(years)) {
# subset to year i
sub <- subset(mothers2534, dataset==years[i])
# prints out year
cat("Year", years[i],"\n")
# prints out average childcare for this group
cat("Average childcare per week:", mean(sub$childtot),"\n")
}Year 1965
Average childcare per week: 13.82249
Year 1975
Average childcare per week: 9.758393
Year 1985
Average childcare per week: 12.86947
Year 1993
Average childcare per week: 9.244037
Year 1998
Average childcare per week: 14.83095
Year 2003
Average childcare per week: 16.02707
Year 2004
Average childcare per week: 16.45709
Year 2005
Average childcare per week: 15.68486
Year 2006
Average childcare per week: 16.23848
Year 2007
Average childcare per week: 17.01327
Year 2008
Average childcare per week: 16.24845 As we can see in this table, this replicates one of the main findings in Ramey and Ramey (2010). In 1965-1993, the average time spent on childcare fluctuated between 9 and 13 hours. From 1998 onwards, the average amount of time spent on childcare increases dramatically, often between 15-17 hours per week on average.
7.5 Tidyverse
So far we have been using what is referred to as base R. We have only utilized functions that come standard in R. However, one of the main strengths of R is its very active user community. Because R is open-source, users can write their own packages in R and make them widely available. This means the functionality of R is essentially growing every day.
One of the most useful collection of packages for data analysis is the tidyverse package. This collection of packages can do many things. We will cover a small portion of what the package is capable of. If you want to get a more thorough understanding of the tidyverse, you can go to R for Data Science and read more.
But before using the tidyverse, we actually have to install it into our version of R. In order to install a package, you can use the install.packages() function. For example, to install tidyverse, type:
install.packages("tidyverse")This will download all the necessary components of the tidyverse package onto your computer. You only need to install a package once.
Next, in order to use a package in a given R session, you need to load it into memory using the library() function:
A common mistake for students is to forget to load a package for a given R session. If you do this, you might get an error such as "[function] not found". If you are using functions from an external package, you need to make sure to load that package in every session of R that you want to use it in.
The first concept we will learn from tidyverse is the concept of a tibble. A tibble is very similar to what we have been calling a data frame. For our purposes, you can think of a tibble as synonymous with data frame. The main difference is in how the data is stored and presented. For us, this won't matter too much. For larger datasets, sometimes loading as a tibble can make a big difference in terms of how long computations take.
To start, let's load rugratrace.csv as a data frame.
rr <- read.csv("rugratrace.csv")To convert a data frame to a tibble, you can use the function as_tibble().
rr <- as_tibble(rr)If you are following along, you may think the code above did not actually do anything. However, you can tell the difference if you print out the data set.
rr
# A tibble: 106,020 × 54
state age sex ethnic under18 under5 ageyngst student
<int> <int> <int> <int> <int> <int> <int> <int>
1 23 26 2 -9 4 2 NA 0
2 23 53 2 -9 1 0 NA 0
3 23 21 2 -9 2 2 NA 0
4 23 24 2 -9 2 2 NA 0
5 23 25 2 -9 3 1 NA 0
6 23 33 2 -9 4 2 NA 0
7 23 26 2 -9 3 2 NA 0
8 23 61 1 -9 0 0 NA 0
9 23 57 1 -9 0 0 NA 0
10 23 43 2 -9 2 1 NA 0
# ℹ 106,010 more rows
# ℹ 46 more variables: act20 <int>, act21 <int>,
# act26 <int>, act24 <int>, act22 <int>, act23 <int>,
# act27 <int>, act67 <int>, act25 <int>, act29 <int>,
# recwght <dbl>, dataset <int>, fips <int>,
# married <int>, working <int>, fulltime <int>,
# parttime <int>, mother2 <int>, father2 <int>, …You get more information printing out a tibble relative to a data frame. For our purposes, it won't matter too much if you load a dataset as a tibble or a data frame. However, it is important to understand these concepts, as you may see various online resources reference a tibble or a data frame. Generally, in this class we will load our datasets as tibbles from now on.
To load a dataset as a tibble directly, you can use the read_csv function, the only difference being now an underscore separates the words in the function, rather than a period.
rr <- read_csv("rugratrace.csv")So now let's discuss some functions that come with tidyverse. The first functions we will introduce are filter, select, and arrange.
The filter() function retrieves observations (rows) in the data that meet a certain condition. For example, maybe you want to restrict the analysis to a certain demographic. You can use the filter() function to do this. In our example, we want to restrict to mothers between ages 25 and 34. We can use filter() to accomplish this. The general syntax for filter() is:
In our example, we can create the subset of the dataset we want by typing:
mothers2534 <- filter(rr, age<=34 & age>=25 & mother2==1)You can use other logical operators in combination with filter as well. For example, imagine for a subset of our analysis we only want years between 2003 and 2008. We can use the operator %in% to accomplish this.
filter(mothers2534, dataset%in%2003:2008)
# A tibble: 6,416 × 54
state age sex ethnic under18 under5 ageyngst student
<int> <int> <int> <int> <int> <int> <int> <int>
1 NA 32 2 NA 1 NA 2 1
2 NA 33 2 NA 3 NA 3 0
3 NA 33 2 NA 1 NA 7 0
4 NA 32 2 NA 1 NA 2 0
5 NA 25 2 NA 1 NA 6 0
6 NA 34 2 NA 2 NA 2 0
7 NA 31 2 NA 1 NA 2 0
8 NA 32 2 NA 2 NA 6 0
9 NA 32 2 NA 2 NA 12 0
10 NA 32 2 NA 2 NA 3 0
# ℹ 6,406 more rows
# ℹ 46 more variables: act20 <int>, act21 <int>,
# act26 <int>, act24 <int>, act22 <int>, act23 <int>,
# act27 <int>, act67 <int>, act25 <int>, act29 <int>,
# recwght <dbl>, dataset <int>, fips <int>,
# married <int>, working <int>, fulltime <int>,
# parttime <int>, mother2 <int>, father2 <int>, …This code is saying restrict to mothers2534 only for observations such that dataset is in the range of 2003 through 2008. One important note here is that in the code above we did not overwrite mothers2534. That is why we can see the tibble being printed out. If you want to save the result of the filter() you need to assign the resulting tibble a name. Otherwise it will simply be printed to the console but not actually saved.
Next, let's discuss select(). This function chooses which variables you want to remain in your tibble. For example, in our current tibble we have many variables, but we really only need a subset of them for our analysis. So we can select the variables we really need:
mothers2534 <- select(mothers2534, dataset, mother2, age, childtot)Now if we print out mothers2534, it has only four variables now.
mothers2534
# A tibble: 8,115 × 4
dataset mother2 age childtot
<int> <int> <int> <dbl>
1 1965 1 26 7
2 1965 1 25 7.58
3 1965 1 33 27.2
4 1965 1 26 4.20
5 1965 1 25 6.42
6 1965 1 26 14.8
7 1965 1 30 19.2
8 1965 1 33 8.75
9 1965 1 30 16.3
10 1965 1 29 29.8
# ℹ 8,105 more rowsFinally, our last function for this section is arrange(). The arrange() function will sort the data based on the values of a variable. For example, imagine I want the observations in mothers2534 to be arranged from the youngest age to the oldest age. I could type:
mothers2534 <- arrange(mothers2534,age)Now, we can verify that the youngest individuals are first:
And the oldest are last.
If you instead want to sort from the oldest to youngest, you can use the function desc(), which stands for descending. In other words, the dataset will be sorted from the highest value to the lowest value.
To finish off this chapter, let's summarize all of the new functions in tidyverse that we learned. First, read_csv() is used in order to read data sets into R as a tibble. Next, we learned three functions that are useful for manipulating data. First, filter() selects observations of the tibble that meet a certain condition. In our case, mothers between the ages 25 and 34. Second, select() chooses which variables to keep in a tibble. In our case, we kept variables that indicated whether an individual is a mother, the year the data was collected, the age of the individual, and the amount of time spent on childcare of the individual. Lastly, arrange() is used to sort the data based on a value of a variable. In this chapter we showed how to use this to sort the data from youngest to oldest.
7.6 The Pipe Operator
In this section we are going to be going over the pipe operator: %>%. The pipe operator is a very useful tool to use when working with the tidyverse. For our purposes, we can use it to string along a number of commands. Eventually, we will see that this greatly improves the efficiency of our code. First, however, we simply need to learn mechanically what the pipe operator does (although why we are using it might not be immediately clear).
So far, in R, we have been applying functions to objects. For example, imagine we have a vector x and we want to take the mean. We would apply the mean() function to x by typing mean(x). The pipe operator gives us an alternative way to write this. We can type: x %>% mean(). In general, when we have a function f(), we can either write f(x) or x %>% f().
So what is the benefit of the pipe operator? Well, often in data analysis, we will want to apply many functions. For example, we may want to restrict to certain observations, select certain variables, and so on. We can think of this as applying many functions to an objects in sequency. For example, if we first apply f(), then g() and then h() we can represent this as:
h(g(f(x)))Using pipe operators, we can equivalently write this out as:
What are we doing here? We are taking in an object x, and then applying f, and then applying g, and then applying h. When you read a pipe operator, you can think to yourself and then. This will be a helpful tool to remember what a pipe operator is doing. It is stringing together a number of different functions in R.
So far, this has been a relatively abstract discussion of pipe operators. Let's load some real data so we can see how this works in practice.
rr <- read_csv("rugratrace.csv")
Rows: 106020 Columns: 54
── Column specification ────────────────────────────────────
Delimiter: ","
dbl (54): state, age, sex, ethnic, under18, under5, agey...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.In a previous chapter, we generated a new data set that (1) filters to mothers between 25 and 34. To understand pipe operators, let's first see how we can perform the same task using %>%.
To remind you, the code to filter from the previous section is:
mothers2534 <- filter(rr, age<=34 & age>=25 & mother2==1)Instead, when we use a pipe operator, we first supply the data frame rr and then call the function (with the relevant logical statement):
This is a useful way to think about the pipe operators when using it with data. First supply the tibble or data frame, and then apply all the functions you would like to the data.
So far, we can't really see the benefit of the pipe operator with this example. It looks as if we have just rewritten the code. The main benefit for the pipe operator for us, however, will be that we can string along multiple commands. For example, imagine we want to (1) filter the data as above, and then (2) select only the variables we need. Before, we did this in two steps:
# filter to mothers 25-34
mothers2534 <- filter(rr, age<=34 & age>=25 & mother2==1)
# select certain variables
mothers2534 <- select(mothers2534, dataset, mother2, age, childtot)These steps are not very efficient. In the first step we create mothers2534. In the next step, we overwrite it with a new mothers2534. In total, we needed to type mothers2534 three different times to get the final tibble. Now, let's see how pipe operators will clean up this code:
mothers2534 <- rr %>%
filter(age<=34 & age>=25 & mother2==1) %>%
select(dataset, mother2, age, childtot)Now the code is a bit easier to digest. What are we doing? First we are specifying the tibble rr, and then we are filtering it, and then we are selecting the variables we want. Now in this example, there are only two steps. But now imagine we want to also sort the dataset from oldest to youngest. No problem, we can just add a pipe operator that calls the arrange() function to the previous code:
mothers2534 <- rr %>%
filter(age<=34 & age>=25 & mother2==1) %>%
select(dataset, mother2, age, childtot) %>%
arrange(desc(age))And our resulting code is still very clear an interpretable. Now imagine you had many, many more steps you needed to perform. You will soon be glad you have the pipe operator!
7.7 Mutate
So far, we have documented that parents increased the amount of time spent on childcare in the 1990s and through the 2000s. Ramey and Ramey (2010) further document that this increase is even more dramatic for college-educated mothers.
Ramey and Ramey (2010) argue the increased time spent on childcare for college-educated mothers is being driven by the competitiveness of college. To provide evidence for this, they break down the components of childcare. Figure 7.2 from Ramey and Ramey (2010) plots the amount of time spent on childcare for college-educated and less-than-college educated mothers by type of care.
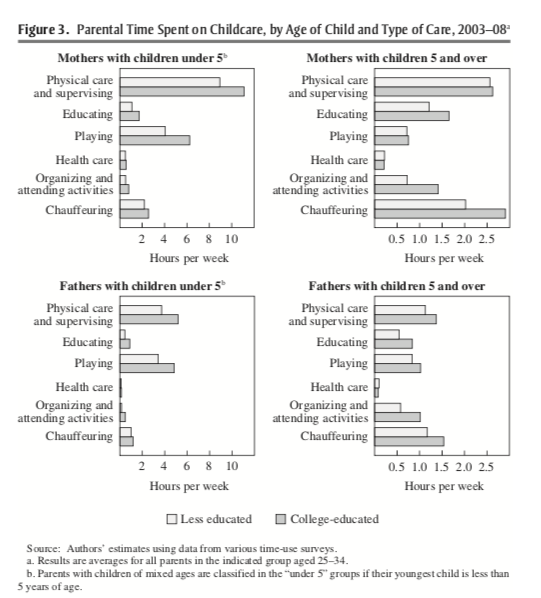
Figure 7.2: Time Spent on Childcare, by Age of Child and Type of Care 2003-2008
Let's focus on the top-right panel: mothers with children above the age of 5. College-educated mothers (the darker gray bars) are spending more time on a few categories: education, organizing and attending activities, and chauffeuring. Ramey and Ramey (2010) argue that these may be driven by college competitiveness. To be competitive in college, students need to earn higher scores on tests and participate in more extracurricular activities.
In our data, we are going to create a variable named childcollegeprep that is the sum total of time spent on education and time spent on travelling with children. Right now, however, our data set does not have this variable. So in order to add this, we will need to learn how to create variables in R.
There are two ways to create new variables in R. The first uses base R. The general syntax is:
df$newvarname <- expressionFor example, let's add the variable childcollegeprep which will be the addition of childeduc and childtravel, which are two variables in our rugratrace.csv data set.
rr$childcollegeprep <- rr$childeduc + rr$childtravel
summary(rr$childcollegeprep)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.000 0.000 0.000 1.201 0.000 98.933 1146 So the mean amount of time spent on childcollegprep is about 1.2 hours. Recall we haven't made any restrictions on rr, so this includes everyone in the data set, including those who don't have children. This explains why the value is so much lower than the values we have been studying for mothers with children in the house.
We can also generate new variables using the mutate() function (from tidyverse). The general syntax is:
mutate(dataframe, newvarname = expression)For example, if we want to add childprep using mutate() we can type:
rr <- mutate(rr, childcollegeprep=childtravel+childeduc)Note that the first step was to type rr <-. If you don't overwrite rr by specifying this step, R will generate a new tibble with the added variable, but it won't be saved anywhere.
A nice thing about mutate() relative to base R is that you can generate a number of variables within the same mutate() command. For example, imagine we also want to create a variable that captures childcare time not spent on college prep. In other words, we want to add the variable childnotcollegeprep = childtot - childcollegeprep to the tibble. We can do this using the following:
rr <- mutate(rr, childcollegeprep=childtravel+childeduc,
childnotcollegeprep=childtot-childcollegeprep)If you have more variables to add or change, you can simply add a comma to the end of the last line, and add the new variable below. Note, we can even call variables that are created earlier in the function (i.e. childnotcollegeprep can only be created if childcollegeprep is created first).
Lastly, let's talk about the transmute() function. This function also generates new variables, but at the same time, it drops all pre-existing variables. For example, if you wanted to create a tibble that only contains childcollegeprep and childnotcollegeprep, you could use the transmute() function:
collegeprepdat <- transmute(rr,
childcollegeprep = childeduc + childtravel,
childnotcollegeprep = childtot - collegeprep)
Error in `transmute()`:
ℹ In argument: `childnotcollegeprep = childtot -
collegeprep`.
Caused by error:
! object 'collegeprep' not foundAs you can see, this is a data set that only contains the two variables we created using transmute().
7.8 Group By and Summarize
Often in the course of our data analysis we will want to break down some summary statistics by some groups. For example, maybe we have a dataset on individual-level voting records and want to compute average voting rates by state. Maybe we have data on wages over time, and we want to compute the average wage by year. In R, a convenient way to make this calculation is by combing the group_by() function with the summarize() function.
To begin our discussion of these functions, we will first illustrate how to use the summarize() command before combining it with group_by(). Our application will again utilize the data from Ramey and Ramey (2010) on time use.
To remind you, the tibble rr contains the year of the observation in a variable named dataset and the amount spent on childcare in a variable named childtot.
The summarize() function is used to generate summary statistics. For example, imagine I just want to take the average level of childtot across the entire sample. We can do this by typing:
The first part of the code, summarize(rr, tells R that we are generating summary statistics from the rr data set. The second, part meanchildtot= is actually giving a name to the summary statistic. In other words, you can change this part of the code and the only difference will be the name on the column that is output. The actual code will still execute without error. This is a helpful feature of the summarize() command because often we will want to save our summary statistics in a new tibble. If there are multiple summary statistics computed, we need to be able to keep track of the various summary statistics. The last part of the code mean(childtot, na.rm=T) is declaring that meanchildtot will be equal to the average of childtot. Because we have specified na.rm=T, missing values are ignored in the computation.
A nice feature of the summarize function is that we can generate multiple statistics in a single line. For example, imagine we would like to compute both the mean level of childcare and the median level of childcare. We can simply add this code to the previous summary command by giving the median a different name:
summarize(rr,
meanchildtot = mean(childtot, na.rm=T),
medianchildtot=median(childtot, na.rm = T))
# A tibble: 1 × 2
meanchildtot medianchildtot
<dbl> <dbl>
1 4.69 0The median is actually zero here because we are taking the median for the entire sample. Many individuals will have zero time spent on childcare, as there aren't any children in many households.
Next, we will discuss the real usefulness of the summarize command: summarizing by groups. Many times as part of our analysis, we might want to provide summary statistics over some group variable. At other times, we may actually want to change the unit-of-observation of our dataset. Using the group_by() function with the summarize() function is a convenient way to accomplish this.
The group_by() function tells R that any subsequent functions should be done separately by the values of the group_by() variable. For example, in our dataset, we have a list of years:
Therefore, if we specify group_by(dataset), then subsequent functions will be applied separately by each value of dataset. In particular, if we next summarize(meanchildtot = mean(childtot, na.rm=T)), then the mean of childtot will be taken separately for each value of dataset. Let's try this all together now.
# A tibble: 14 × 2
dataset meanchildtot
<dbl> <dbl>
1 1965 4.27
2 1975 3.36
3 1985 2.95
4 1993 2.09
5 1995 4.23
6 1998 5.20
7 2000 10.5
8 2003 4.85
9 2004 4.73
10 2005 5.17
11 2006 5.06
12 2007 4.92
13 2008 4.97
14 NA NaN The way we can read the code above is: first read in rr tibble, and then group by values of the variable dataset, and then for each value of dataset, take the average of childtot, and store this information under the name meanchildtot.
We can also make this even more complicated by summarizing by two variables. If you type group_by(var1,var2), then R will group by the unique combination of variables. Before proceeding to the main example, let's generate a small data frame through which we can understand grouping by two variables.
student.df <- data.frame(school=c("A", "A", "A", "B", "B", "B"),
graduationdate=c(2010,2010,2015,2010,2010,2015),
gpa = c(3.2,3.7,2.9,4.0,3.2,1.8))student.df
school graduationdate gpa
1 A 2010 3.2
2 A 2010 3.7
3 A 2015 2.9
4 B 2010 4.0
5 B 2010 3.2
6 B 2015 1.8If I type group_by(school,graduationdate), then any subsequent summarize() command will be done completely separately by unique combinations of school and graduationdate. In this data frame, there are 4 unique combinations -- "A 2010", "A 2015", "B 2010", "B 2015". So let's see what we get when we summarize by groups of two variables:
student.df %>%
group_by(school,graduationdate) %>%
summarize(mean.gpa=mean(gpa))
`summarise()` has grouped output by 'school'. You can
override using the `.groups` argument.
# A tibble: 4 × 3
# Groups: school [2]
school graduationdate mean.gpa
<chr> <dbl> <dbl>
1 A 2010 3.45
2 A 2015 2.9
3 B 2010 3.6
4 B 2015 1.8 To understand how the unique combinations are generated, let's change the dataset slightly.
student.df <- data.frame(school=c("A", "A", "A", "B", "B", "B"),
graduationdate=c(2010,2010,2010,2015,2015,2015),
gpa = c(3.2,3.7,2.9,4.0,3.2,1.8))Now there are only two unique combinations in the data of school and graduation date: "A 2010" and "B 2015". Therefore, when we summarize by groups, there will be only two averages taken:
student.df %>%
group_by(school,graduationdate) %>%
summarize(mean.gpa=mean(gpa))
# A tibble: 2 × 3
# Groups: school [2]
school graduationdate mean.gpa
<chr> <dbl> <dbl>
1 A 2010 3.27
2 B 2015 3 Now, let's return to the rr tibble. In Ramey and Ramey (2010), the authors compared time spent on childcare over time separately for college-educated and less-than-college educated individuals. We can achieve a similar analysis by grouping over dataset and college. The variable college is a variable that takes on a value of 1 if the individual graduated from college, and zero otherwise.
rr %>%
group_by(dataset,college) %>%
summarize(meanchildtot = mean(childtot, na.rm=T))
# A tibble: 27 × 3
# Groups: dataset [14]
dataset college meanchildtot
<dbl> <dbl> <dbl>
1 1965 0 4.35
2 1965 1 3.66
3 1975 0 3.33
4 1975 1 3.51
5 1985 0 2.89
6 1985 1 3.13
7 1993 0 2.25
8 1993 1 1.74
9 1995 0 4.39
10 1995 1 3.85
# ℹ 17 more rowsTo understand this table, let's look at the first row of data. This first row has dataset==1965 and college==0. In other words, this row corresponds to individuals in 1965 without a college education. The value in the meanchildtot column is the average amount of time spent on childcare for these individuals. If we move down this table, we will see R has computed the mean time spent on childcare for every unique combination of dataset and college.
Often in practice, we may want to actually save the output of this function. To do so, we just need to assign it a name, as usual:
totchildbyyearcollege <- rr %>%
group_by(dataset, college) %>%
summarize(meanchildtot = mean(childtot, na.rm=T))Now we have created a new tibble totchildbyyearcollege that contains these averages over time by college education.
We could have also accomplished this by looping over values of dataset and college and then computing the means and storing them. But doing so would have included (1) writing much more code and (2) would have actually taken longer to run. Using group_by() with summarize() is a much more efficient way to accomplish this.
7.9 Conclusion
In this final section we will put all the various functions we've learned together into one analysis. As a reminder, our goal is to compute the average time spent on childcare for mothers over time, separately by college-education status. In other words, replicate Figure 7.1 from Ramey and Ramey (2010) which shows increased time spent on childcare beginning in the 1990s, especially for college-educated mothers.
This review will focus on the tidyverse package. As a reminder, the first time using a package you need to install it using install.packages("packagename"). You only need to do this once. However, every time you want to use the package in a given R session, you need to load it into memory using the library() function. For example, to load tidyverse we would type:
libary(tidyverse)To begin, let's first re-load our data into R as a tibble using the read_csv() function. The read_csv() function reads in a dataset as a tibble, while the read.csv() function reads the dataset into memory as a data frame. For our purposes, there won't be too much differences between these formats, but tibbles will be more efficient with large datasets.
rr <- read_csv("rugratrace.csv")
Rows: 106020 Columns: 54
── Column specification ────────────────────────────────────
Delimiter: ","
dbl (54): state, age, sex, ethnic, under18, under5, agey...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Our first issue is that the Ramey and Ramey (2010) analysis was for a particular group of individuals: mothers aged 25-34. Therefore, we first need to create a dataset restricted to these individuals. We can achieve this by using the filter() function.
mothers2534 <- filter(rr, mother2==1, age>24, age<35)Now, a focus of our analysis will be what is driving the increase in time spent on childcare. One potential driver is increased time spent on college prep activities, given an increase in the competitiveness of college during this time. We are going to add a variable named collegeprep to this dataset which is the time spent either on traveling with children or time spent educating children.
mothers_collegeprep <- mutate(mothers2534,
collegeprep = childeduc + childtravel)Our goal is to compute the amount of time spent on collegeprep over time, by college education status. We can accomplish this by using group_by() and summarize() functions together.
collegeprep <- mothers_collegeprep %>%
group_by(dataset, college) %>%
summarize(meancollegeprep=mean(collegeprep, na.rm=T))
`summarise()` has grouped output by 'dataset'. You can
override using the `.groups` argument.Now if we look at our resulting tibble, we can use it to understand trends in time spent on college prep over time:
print(collegeprep,n=25)
# A tibble: 22 × 3
# Groups: dataset [11]
dataset college meancollegeprep
<dbl> <dbl> <dbl>
1 1965 0 2.14
2 1965 1 1.88
3 1975 0 1.66
4 1975 1 1.69
5 1985 0 2.52
6 1985 1 2.72
7 1993 0 1.49
8 1993 1 1.87
9 1998 0 2.46
10 1998 1 2.51
11 2003 0 3.27
12 2003 1 3.34
13 2004 0 2.87
14 2004 1 3.72
15 2005 0 3.23
16 2005 1 3.05
17 2006 0 3.00
18 2006 1 3.16
19 2007 0 3.18
20 2007 1 3.30
21 2008 0 3.39
22 2008 1 3.28What do we find in this data? In the 60s-70s, on average, mothers spent around 1.5-2 hours on activities that may be related to college preparation. This increases over time, and by the 2000s, it has stabilized to closer to 3 hours on average. Therefore, we find something broadly consistent with Ramey and Ramey (2010). Time spent on childcare has increased over time, and in particular, for activities that may be related to college preparation.
Now, one thing to note is that we have done this analysis step-by-step. First we restricted our sample, then we added the variables, and lastly we summarized by group. However, we could have also done this entire analysis in a single block of code by stringing together functions using the pipe operator, as is done below:
collegeprep <- rr %>%
filter(mother2==1, age>24, age<35) %>%
mutate(collegeprep = childeduc + childtravel) %>%
group_by(dataset, college) %>%
summarize(meancollegeprep=mean(collegeprep, na.rm=T))
`summarise()` has grouped output by 'dataset'. You can
override using the `.groups` argument.Going forward in the book, the tools we have learned in this section will be very important. It is extremely common to need to perform some data wrangling steps before proceeding to your actual analysis. The tidyverse package has given us a convenient set of functions in order to perform this analysis.
Function Descriptions
Tidyverse Functions
read_csv()-- Reads a csv into memory as a tibble. A tibble is similar to a data frame, but more efficient in many settings.as_tibble()-- Converts a data frame to a tibble.filter()-- Restricts to certain observations in a data set. For example,filter(df, age>18)would restrict the hypothetical data framedfto individuals withage>18.arrange()-- Sorts the data based on the value of a variable. For example,arrange(df, age)would sort the datasetdffrom youngest to oldest.select()-- Selects certain variables from a dataset. It can be used to restrict to only the variables needed for your analysis.mutate()-- used to generate new variables.group_by()-- Groups data based on values of a variable. Any subsequent commands will be done separately by the values of the variable.summarize()-- Used to generate summary statistics. Often combined withgroup_by()in order to generate summary statistics by groups.
Other Functions
sample()-- Draws a random number from a list of numbers. For example,sample(-1:1,1)draws a single number from the list of numbers-1:1. In other words, it will draw a random number from -1 to 1.sample(c(0,1,2),4)would draw 4 random numbers from the list of numbers 0,1, or 2.cat()-- Concatenates text in R. For example,cat("Hello","World")will yield the phrase "Hello World".unique()-- Retrieves a list of the unique values a variable takes on.
Installing/Loading Functions
install.packages()-- Installs a package onto your version of R. For example,install.packages("tidyverse")will install the tidyverse into R. You need to install a package once.library()-- Loads a package into memory.